| Squeeze the Memory Consumption of Deep Learning |
| =============================================== |
| One important theme about deep learning is to train deeper and larger nets. |
| While the hardware has been upgraded rapidly in recent years, the huge deepnet monsters are |
| always hungry about the GPU RAMS. Being able to use less memory for the same net also means we can |
| use larger batch size, and usually higher GPU utilization rate. |
| |
| This article discusses how memory allocation optimization can be done for deep neural nets, and provide |
| some of candidate solutions to the problems. The solutions discussed in this article is by no means complete, |
| but rather as example that we think is useful to most cases. |
| |
| Computation Graph |
| ----------------- |
| We will start the discussion by introducing computation graph, since this is the tool that will help us in the later |
| part of the section. Computation graph describes the (data-flow) dependencies between the operations in the deep nets. |
| The operation performed in the graph can either be fine-grained or coarse grained. |
| The following figure gives two examples of computation graph. |
| |
| 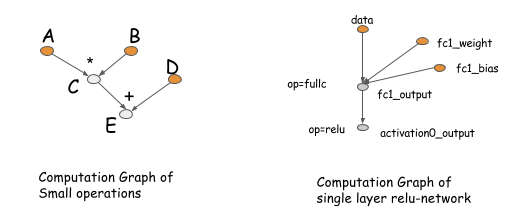 |
| |
| The idea of computation graph is deeply rooted in the packages such as Theano, CGT. Actually they also exists implicitly |
| in most libraries as the network configuration. The major difference in these library comes to how do they calculate gradient. |
| There are mainly two ways, doing back-propagation on the same graph, or have an explicit backward path that calculates |
| the gradient needed. |
| |
| 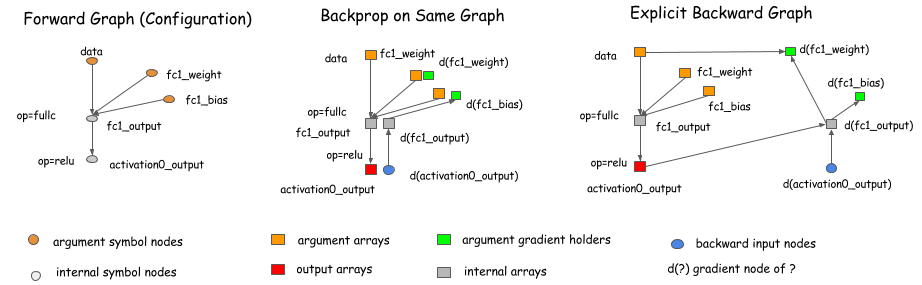 |
| |
| Libraries like caffe, cxxnet, torch uses the backprop on same graph. While libraries like Theano, CGT takes the explicit |
| backward path approach. We will adopt the ***explicit backward path*** way in the article, because it brings several advantages |
| in turns of optimization. |
| |
| However, we should emphasize that choosing the explicit backward path way for execution will not restrict us |
| to scope of symbolic libraries such as Theano, CGT. We can also use the explicit backward path for gradient calculation of |
| layer-based(which ties forward, backward together) libraries. The following graph shows how this can be done. |
| Basically, we can introduce a backward node that links to the forward node of the graph, and calls the ```layer.backward``` |
| in the backward operations. |
| |
| 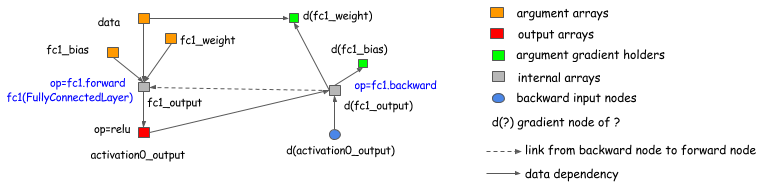 |
| |
| So this discussion applies to almost all deep learning libraries that exists |
| (There are differences between these libraries, e.g. high order differentiation. which are beyond the scope of in this article). |
| |
| Why explicit backward path is better? Let us explain it with two examples. The first reason is that the explicit backward path |
| clearly describes the dependency between the computation. Consider the following case, where we want to get |
| the gradient of A and B. As we can see clearly from the graph, that computation of ```d(C)``` gradient do not depend on F. |
| This means we can free the memory of ```F``` right after the the forward computation is done, similarly the memory |
| of ```C``` can be recycled. |
| |
| 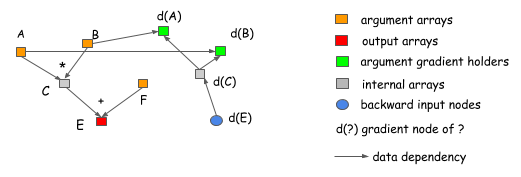 |
| |
| Another advantage of explicit backward path is to be able to have a different backward path rather than an mirror of forward one. |
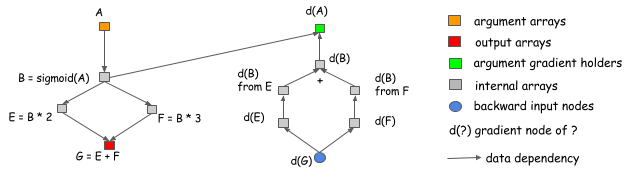
| One common example is the split connection case, as shown in the following figure. |
| |
|  |
| |
| In this example, the output of B is referenced by two operations. If we want to do the gradient calculation in the same |
| network, an explicit split layer need to be introduced. This means we need to do the split for the forward pass as well. |
| In this figure, the forward pass do not contain a split layer, but the graph will automatically insert a gradient |
| aggregation node before passing gradient back to B. This helps us to save the memory cost of allocating output of |
| split layer, as well as operation cost of replicate the data in forward pass. |
| |
| If we adopt the explicit backward view of computation graph, there is no difference between the forward pass |
| and backward pass. We will simply go forward in topological order of the computation graph, and carry out computations. |
| This also simplifies our discussions. The problem now becomes: |
| |
| - How to allocate the memory of each output node of a computation graph? |
| |
| Hmm, seems it has nothing to do with deep learning, but more of context of compiling, data flow optimization etc. |
| But it is really the hungry monster of deep learning that motivates us attack this problem, and benefit from it. |
| |
| What can be Optimized |
| --------------------- |
| Hopefully you are convinced that the computation graph is a good way to discuss memory allocation optimization techniques. |
| As you can see some memory saving can already been bought by using explicit backward graph. Let us discuss more about |
| what optimization we can do, and what is the baseline. |
| |
| Asumme we want to build a neural net with ```n``` layers. A typical implementation of neural net will |
| need to allocate node space for output of each layer, as well as gradient values for back-propagation. |
| This means we need roughly ```2 n``` memory cells. This is the same in the explicit backward graph case, as |
| the number of nodes in backward pass in roughly the same as forward pass. |
| |
| ### Inplace Operations |
| One of the very first thing that we can do is inplace memory sharing of operations. This is usually done for |
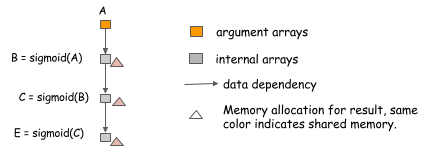
| simple operations such as activation functions. Consider the following case, where we want to |
| compute the value of three chained sigmoid function. |
| |
|  |
| |
| Because we can compute sigmoid in the ```inplace``` manner, that is, use the same memory for input and output. |
| We can simply allocate one copy of memory, and use it compute arbitrary length of sigmoid chain. |
| |
| However, the inplace optimization sometimes can be done in the wrong way, especially when the package tries |
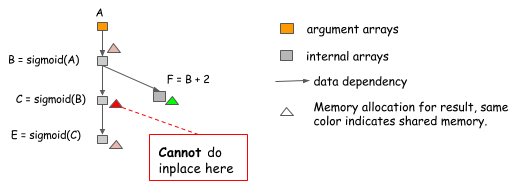
| to be a bit general. Consider the following case, where the value of B is not only used by C, but also F. |
| |
|  |
| |
| We cannot perform inplace optimization because the value of B is still needed after ```C=sigmoid(B)``` is computed. |
| So an algorithm that simply do inplace optimization for every sigmoid operation might fall into such trap, |
| and we need to be careful on when we can do it. |
| |
| ### Normal Memory Sharing |
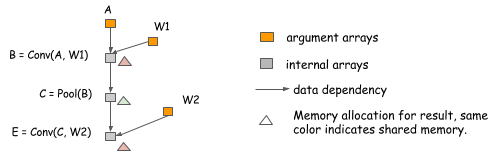
| Memories can also be shared besides the inplace operation. Consider the following case, because the |
| value of B is no longer needed when we compute E, we can reuse the memory to hold the result of E. |
| |
|  |
| |
| We would like to point out that is ***memory sharing does not necessarily require same data shape****. |
| In the above example, the shape of ```B``` and ```E``` can be different, and we can simply allocate a |
| memory region that is the maximum of the two sizes and share it between the two. |
| |
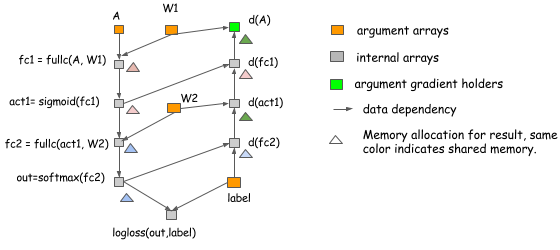
| ### Real Neural Net Allocation Example |
| The above examples are all make up cases, that only contains the computation of the forward pass. |
| Actually the idea holds the same for the real neural net cases. The following figure shows an allocation |
| plan we can do for a two layer perception. |
| |
|  |
| |
| In the above example: |
| - Inplace optimization is applied on computing ```act1```, ```d(fc1)```, ```out``` and ```d(fc2)```. |
| - The memory sharing is used between ```d(act1)``` and ```d(A)```. |
| |
| Memory Allocation Algorithm |
| --------------------------- |
| We have discussed how the general techniques to optimize memory allocations in previous section. |
| However, we also see that there are traps which we want to avoid like the inplace case. |
| How can we allocate the memory correctly? This is not a new problem. For example, it is very similar |
| to register allocation in compilers. So there could be a lot we can borrow. We do not attempt to give |
| a comprehensive review of techniques here, but rather introduce some simple but useful trick to attack |
| the problem. |
| |
| The key problem is we want to place resources, such that they do not conflict each other. |
| More specifically, each variable have a ```life time``` between the time it get computed till the last time it get used. |
| In the multilayer perception case, the ```life time``` of ```fc1``` ends after ```act1``` get computed. |
| |
|  |
| |
| The principle is ***to only allow memory sharing between the variables whose lifetime do not overlap***. There are multiple |
| ways to solve this problem. One possible way is to construct the conflicting graph of with each variable as node and link edge |
| between variables with overlapping lifespan, and run a graph-coloring algorithm. This will likely require ```$O(n^2)$``` |
| complexity where ```n``` is number of nodes in the graph, which could be an reasonable price to pay. |
| |
| We will introduce another simple heuristic here. The idea is to simulate the procedure of traversing the graph, |
| and keep a counter of future operations that depends on the node. |
| |
| 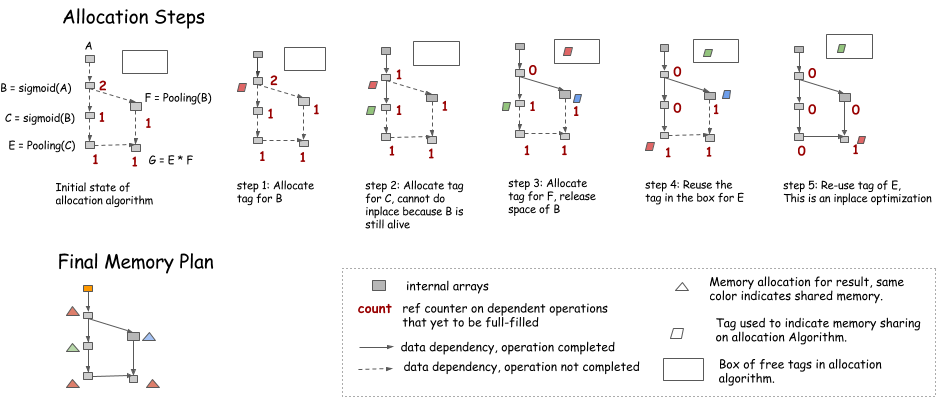 |
| |
| - An inplace optimization can be performed when only current operation depend on the source(i.e. counter=1) |
| - A memory can be recycled into the box on the upper right corner when counter goes to 0 |
| - Every time, when we need new memory, we can either get it from the box, or allocate a new one. |
| |
| One note is that during the simulation, no memory is allocated, but we rather keep record of how much memory each node need, |
| and allocate the maximum of the shared parts in the final memory plan. |
| |
| ### Static vs Dynamic Allocation |
| |
| If you think carefully, you will find the above strategy exactly simulates the dynamic memory allocation procedure in imperative |
| languages such as python. The counter is the reference counter of each memory object, and the object get garbage collected when |
| the reference counter goes to zero. In that sense, we are simulating the dynamic memory allocation once to create a static allocation plan. |
| Now the question is, can we simply use an imperative language that dynamically allocates and de-allocates memories? |
| |
| The major difference is that the static allocation is only done once, so we can afford to use more complicated algorithms |
| - For example, do searching over memories sizes that are similar to the require memory block. |
| - The allocation can also be made graph aware, see more discussion in next section. |
| - The dynamic way will push more pressure on fast memory allocator and garbage collector. |
| |
| There is also one takeaway for users who want to reply on dynamic memory allocations: |
| ***do not take unnecessary reference of object***. For example, if we organize all the nodes in |
| a list and store then in a Net object, these nodes will never get de-referenced, getting us no gain of the space. |
| Unfortunately, this is one common way to organize the code. |
| |
| |
| Allocation for on Parallel Operations |
| ------------------------------------- |
| In the previous section, we discussed how we can ```simulate``` the running procedure of computation graph, |
| and get a static allocation plan. However, there are more problems when we want to optimize for parallel computation |
| as resource sharing and parallelization are on the two ends of a balance. |
| Let us look at the following two allocation plan for the same graph: |
| |
| 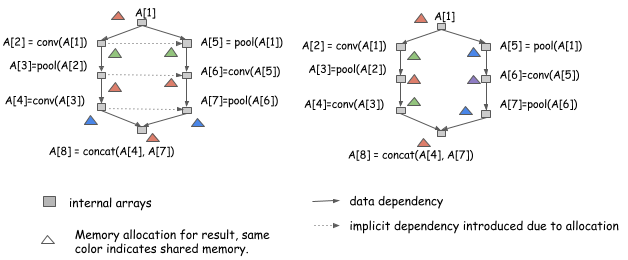 |
| |
| Both allocation plans are valid, if we run the computation in a serial manner from ```A[1]``` to ```A[8]```. |
| However, the allocation plan on the left side introduces extra dependencies, which means we cannot |
| run computation of ```A[2]``` and ```A[5]``` in parallel, while the right one can. |
| |
| As we can see that if we want to parallelizing the computation, more care need to be done in terms of computation. |
| |
| ### Stay Safe and Correct First |
| Stay correct, this is the very first principle we need to know. This means execute in a way to take the implicit dependency |
| memory sharing into consideration. This can done by adding the implicit dependency edge to execution graph. |
| Or even simpler, if the execution engine is mutate aware as described in the |
| [dependency engine note](http://mxnet.readthedocs.org/en/latest/developer-guide/note_engine.html), push the operation |
| in sequence and write to the same variable tag that represents the same memory region. |
| |
| Another way is always produce memory allocation plan that is safe, which means never allocate same memory to nodes that can |
| be parallelized. This may not be the ideal case, because sometimes memory reduction is more desirable, and there is not too |
| much gain we can get by multiple computing stream execution on the same GPU. |
| |
| ### Try to Allow More Parallelization |
| Given that we can always be correct, we are now safe to do some optimizations. The general idea is to try to |
| encourage memory sharing between nodes that cannot be parallelized. This again can be done by creating a ancestor relation |
| graph and query this during allocation, which cost around ```$O(n^2)$``` time to construct. We can also use heuristic here, |
| for example, one way is to color the path in the graph. |
| The idea is shown in the figure below, every time we tries to find a longest path in the graph, color them to same color, |
| and continue. |
| |
| 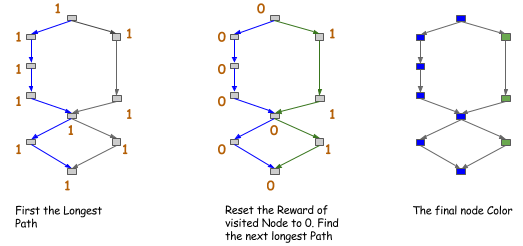 |
| |
| After we get the color of the node, we can only allow sharing (or encourage such sharing ) between nodes in the same color. |
| This is a more strict version than the ancestor relation, but only cost ```$O(n)$``` time if we only search for first ```k``` path. |
| |
| The strategy discussed here is by no means the only solution, we can expect more sophisticated approaches along this line. |
| |
| How much can We Save |
| -------------------- |
| Thanks for reading till this part! We have discussed the techniques and algorithms we can use to squeeze the memory usage of deep learning. |
| Now comes the question on how much we can really save by using these techniques. |
| |
| The answer is we can roughly reduce the memory consumption ***by half*** using these techniques. This is on the coarse grained operation graphs that are already optimized with big operations. More memory reduction could be seen if we are optimizing a fine-grained computation network used by symbolic libraries such as Theano. |
| |
| Most of the ideas in this article inspires the design of mxnet. |
| We provide an [Memory Cost Estimation Script](https://github.com/dmlc/mxnet/tree/master/example/memcost), |
| which you can play with to see how much memory we need under different strategies. |
| |
| If you play with the script, there is one option called ```forward_only```, which shows the cost only running the forward pass. |
| You will find that the cost is extremely low compared to others. You won't be surprised if you read previous part of |
| the article, this is simply because more memory re-use if we only run the forward pass. So here are the two takeaways: |
| |
| - Use computation graph to allocate the memory smartly and correctly. |
| - Running deep learning prediction cost much less memory than deep learning training. |
| |
| Contribution to this Note |
| ------------------------- |
| This note is part of our effort to [open-source system design notes](http://mxnet.readthedocs.org/en/latest/#open-source-design-notes) |
| for deep learning libraries. You are more welcomed to contribute to this Note, by submitting a pull request. |
| |